B树(Btree)
数据库数据查找算法演变:(B+Tree索引的由来)
这个举个简单的例子,假设现在一个教室中有100来号人,这时可以派发礼品,通过礼品引诱这100人来报名学习xiaoQ老师课程;
比如礼品是学习课程的1000元代金券,现在把这1000元的代金券随机放到了1到100号盒子其中的一个里面,只有我知道放置的号码;
下面要求这100个人尽量快的猜到1~100号盒子里面,哪个有放置代金券的盒子,当然,我会给予一些合适的提示信息;
这时在场的100号人就需要想一些办法,在我合适的配合下,定位有代金券的盒子,想的办法就等价于是查找算法:
方法一:根据定位的盒子编号顺序,询问是与否,这种方式就可以理解为是遍历算法(全扫描),也可以理解为随机性算法;
方法二:根据定位的盒子编号比较,询问大于小,这种方式就可以理解为是二分算法(定范围),也可以理解为二叉树算法;
看似这种二分算法比遍历算法,更加科学,但是如果代金券放在了第01号或第100号盒子里呢,或者二分节点两侧时呢?
所以采用二分法依然会存在数据查询不平衡的问题。
通过以上两种算法的介绍,了解到都存在一些缺陷或问题,因此数据库在检索数据信息时,最终采用的算法是B+Tree,其中的B表示平衡
并且BTREE还可以细分为B-tree或B+tree,以及B++tree,其中的加号就是表示增强版或优化版的BTree
对于B++tree算法的底层算法逻辑理解:
利用Btree算法还是快速锁定100个盒子中,有代金券的盒子编号,如下图所示:
- 将需要存储的数据信息,均匀分配保存到对应页当中,最终数据信息的均匀存储(落盘)
- 根据页节点存储的数据信息,取出页节节点最小数据信息,并将每个叶节点最小数据信息进行汇总整合,生成相应内部节点数据;实质上存储的是下层页节点的区间范围,以及与之对应的指针信息,最后构建出内部节点信息;
- 根据内部节点存储的数据信息,取出内部节点最小数据信息,并将每个内部节点最小值信息进行汇总整合,生成相应根节点数据;根节点只能有占用一个页区域,如果一个页区域空间不够,需要进行内部节点层次扩展,但是尽量要保证层次越少越好;
实质上存储的是下层内部节点的区域范围,以及与之对应的指针信息,最后构建出独立且唯一的根节点信息;
- 整个树形结构,越向上节点存储数据的范围越大,然后依次再分发数据到下面的小范围,最终形成多叉树;由于出现了多叉树,就表示全部数据分布在多个链表上,避免了单条链表存储数据,同时可以实现并发的访问数据
- 对于加号表示增强,其中增强表示在整个链表上,增加了同级相邻节点之间的双向指针,从而实现相邻节点相互跳转
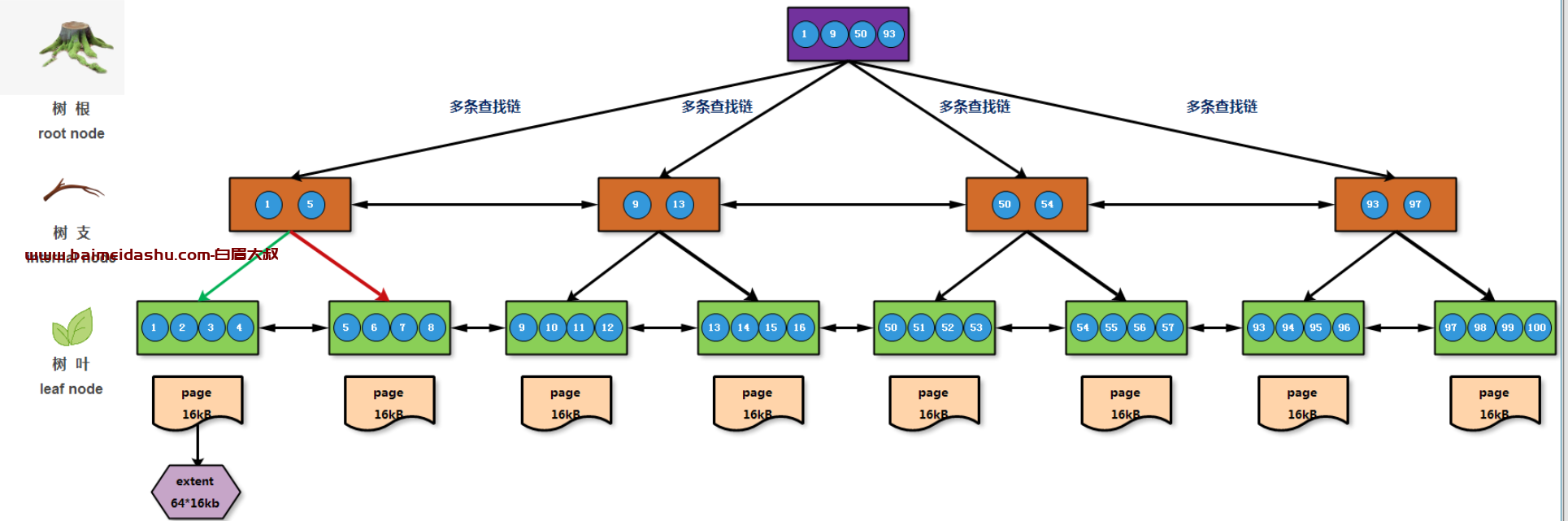
根据以上B+Tree的结构说明,假设现在需要查找54这个数据值信息所在的数据页:等值查询
- 根据定义查找的数值信息,首先在根节点中获取数值所在的区间范围和相应指针信息,从而找到下层对应的内部节点信息;
- 根据定义查找的数据信息,其次在枝节点中获取数值所在的区域范围和相应指针信息,从而找到下层对应的叶子节点信息;
- 根据定义查找的数据信息,最后在叶子节点中获取最终的数据信息,结果结合上图经历三步完成了数据查找(3*16=48kB);
在利用BTree查找数据信息时,会结合树形层次结构,来决定查询数据的步骤过程,并且理论上每个数据查找过程步骤相同;
总结:B代表的平衡含义 balance就是,每次查找数据消耗的IO数量是一致的,并且读取的页数量也是一致的,查找时间复杂度是一致的;
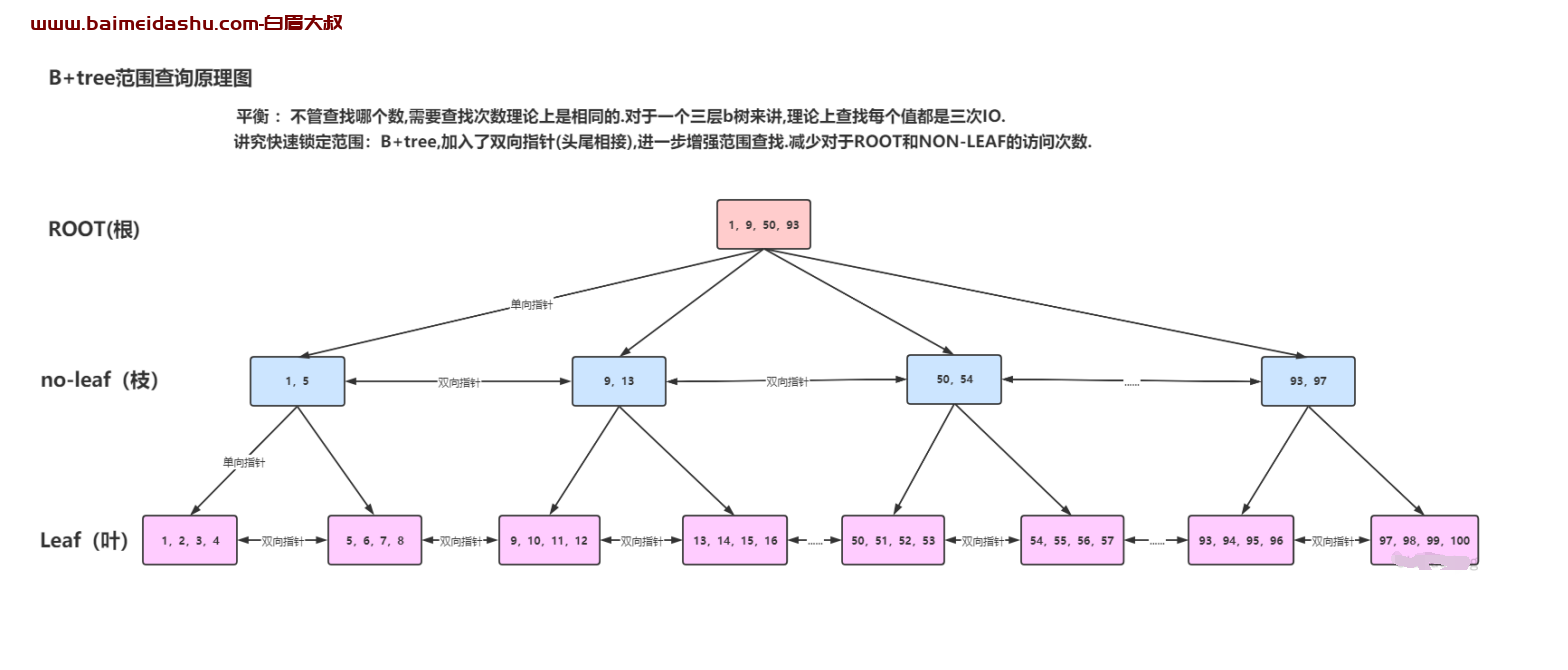
根据以上B+Tree的结构说明,假设现在需要查找大于90这个数据值信息所在的数据页:不等值查询
- 根据定义查找的数值信息,首先在根节点中获取首个大于指定数值的区间范围和相应指针信息,从而找到下层对应的内部节点信息;
- 根据定义查找的数据信息,其次在枝节点中获取数值所在的区域范围和相应指针信息,并且结合双向指针进行预读;
- 根据定义查找的数据信息,最后在叶子节点中获取最终的数据信息,并且结合双向指针进行预读,查询其余大于90的数值;
在利用BTree查找数据信息时,由于存在双向指针概念,可以避免重复从根查找问题,减少IO消耗,结合预读快速调取数据到内存中
总结:在BTree中的双向链接增强特性和预读功能,可以根据簇(64page)读取数据,可以使数据信息的范围查找变得更加方便高效
欢迎来撩 : 汇总all